序
虽然经验告诉我们’眼见为实’,但眼睛告诉我们的’真想’或许隐瞒了部分事实,或许夸大了事实.
统计这种神秘的语言,在一个靠数字说话的社会里是如此地吸引眼球,但有时它却被人利用,并成为恶意夸大或简化事实,迷惑他人的工具.
该书是一个利用统计数据行骗的入门书籍.
样本偏离
统计数字的样本经常存在严重偏离的情况.会接受抽样调查的人,某种意义上已经进行了一部分情景化的过滤.
样本碍于情面或者是尊严的问题,未必会说真话.
小结
- 为了确保结论有价值,根据抽样得出的结论一定要采用具有代表性的样本,这种样本才有可能排除误差
- 无形的误差和有形的误差一样容易破坏样本的可行度.
- 最基本的样本是随机样本,它是完全遵循随机原则从总体总选出来的.随机样本的校验方法:总体中的每个名字或每个事物是否具有相同的几率被选进样本?
- 一般而言,民意调查都具有一定的误差.
精心挑选的平均数
- 平均数:一组数据的总和除以这组数据个数所得到的商叫这组数据的平均数.
- 中位数:将一组数据按大小顺序排列,处在最中间位置的一个数叫做这组数据的中位数 .
- 众数:在一组数据中出现次数最多的数叫做这组数据的众数.

当你看到某个平均收入时,首先问问:是什么的平均?包括了哪些人?
没有披露的数据
有时候单凭一个数据,如平均数来描述事物过于简单,起不到作用,不管这个平均数是均值还是中位数,也不管平均数的具体类型是否已知.需要关注其他未披露的数据,才能判断统计数据的准确性.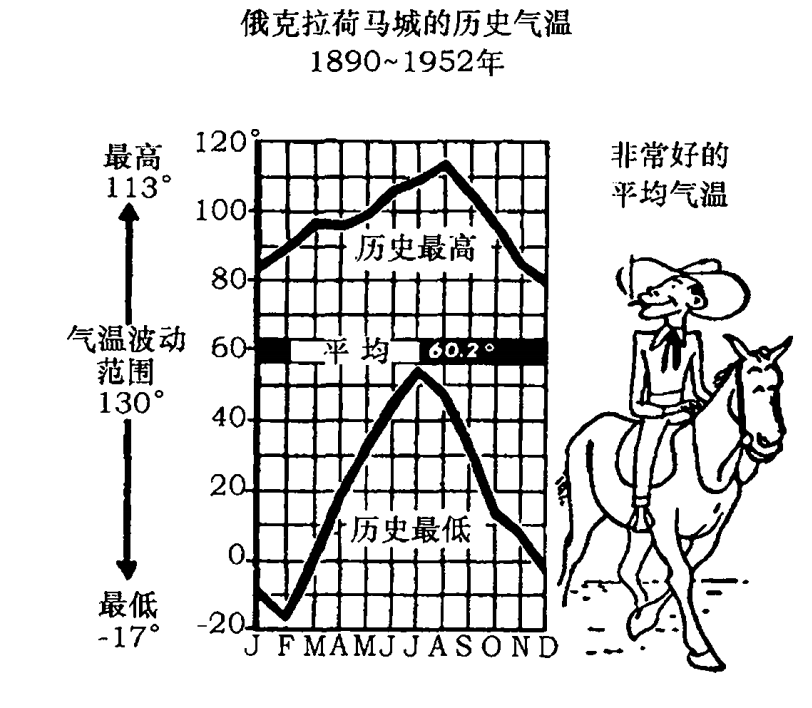
令人惊奇的图形
- 最简单的图形是直线图形,在显示趋势时,直线图形非常有用.然而只需要改变纵坐标和横坐标的比例关系,将会产生一张有迷惑作用的统计图形.统计图形具有客观性幻觉.
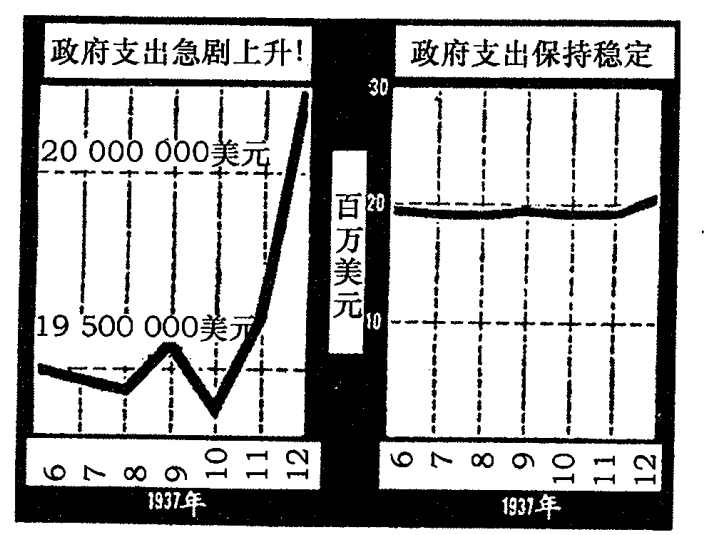
- 用图形描述统计事物,具有欺骗性,视觉作用起了非常大的作用.如数字比是2:1,但视觉效果却是4:1,而在大多数时候视觉效果起着决定性的作用.

相关关系的误解
- 两个事物之间的关联关系并不能用于说明其中一个将引起另外一个的变化.
如何反驳统计资料
怎样凭借双眼就能识破虚假的统计资料,并揭开它的老底;同样重要的是,如何在这一大片充满了欺骗性的数据海洋中找出可靠有用的资料,我们只需要问5个问题.
谁说的?
学术结论,实验结果以及报道引用都可能产生偏差,这些偏差可能是测量标准的改动造成的,也可能是不正确的测量方法造成的.
- 查看有意识的偏差.
- 查找无意识的偏差.
- 如引用到了权威人士,辨明内容是权威的还是资料是权威的.
它是如何知道的?
- 看样本是否有偏离.
- 采样数据是否足够大,观察值是否足够,从而保证结论的可靠性?
遗漏了什么?

- 很多数据由于没有进行有效的比较而失去意义
- 有时仅给出百分比却缺少原始数据也会造成欺骗.当看到一个指数时,需要了解它的基数.
- 遗漏了引起变化的原因,这容易让人认为是其他的因素才应对产生的变化负责.
如报道’最近25年癌症死亡人数增多’,这个结论会有误导性.事实上人口也在增多.
是否有人偷换了概念?
数据的概念是否存在欺诈性?需要留心从搜集原始资料到形成结论的整个过程中,是否存在概念的偷换.
这个资料有意义吗?
这个问题通常能将一个伪装的很好的统计资料打回原形.让人印象深刻的统计数据也会和实际情况相左.
- 奇妙的数据与平常的感觉不符
- 外推法十分有用,特别是预测趋势时.
